コレクション 三角 関係 図 344346

図1 治療における三角関係 患者－医師関係に家族が深く関わることを図式化している。二者関係は幻想であり、 本当は三角関係となる。 図2 直線モデル（単一原因と複数原因）に対するシステムモデルの図式化 生物医学では直線モデルで説明可能だが、家族志向のケアではシステムの中での31 三角比 131 312 三角比の相互関係 直角三角形では3辺の長さの関係として，三平方の定理が成り立つ．ここでは，三 角比sinµ，cosµ，tanµ の間に，どのような関係が成り立つかを調べてみよう． A 三角比の相互関係 右の図の直角三角形ABCにおいて x = rcosµ第三角法のマーク 図面は採用した投影法が分かるようにマークを記載するルールとなっています。 日本ではjisで第三角法を採用して作図することになっているため、下図に示すマークを図枠内に配置する必要があります。

三角関係の写真素材

三角 関係 図

三角 関係 図-図の下のスライダーを動かすと， \(\theta\) の値が変化します。 この図から，次の関係の成り立つことが分かります。 \\sin(\theta) = \sin\theta,\quad \cos(\theta) = \cos\theta\オグデン／リチャーズ共著、石橋幸太郎訳『意味の意味』（新泉社 一九八八）にふつう「意味の三角形」と呼ばれる、下記のような三角形が示されています。 この図に関しては、同書にはつぎのように記されています。 〈思想と象徴との間には因果関係が支配する。 われわれが談話に用いる象徴体系は、一部はわれわれの行う指示により、また一部は社会的、心理

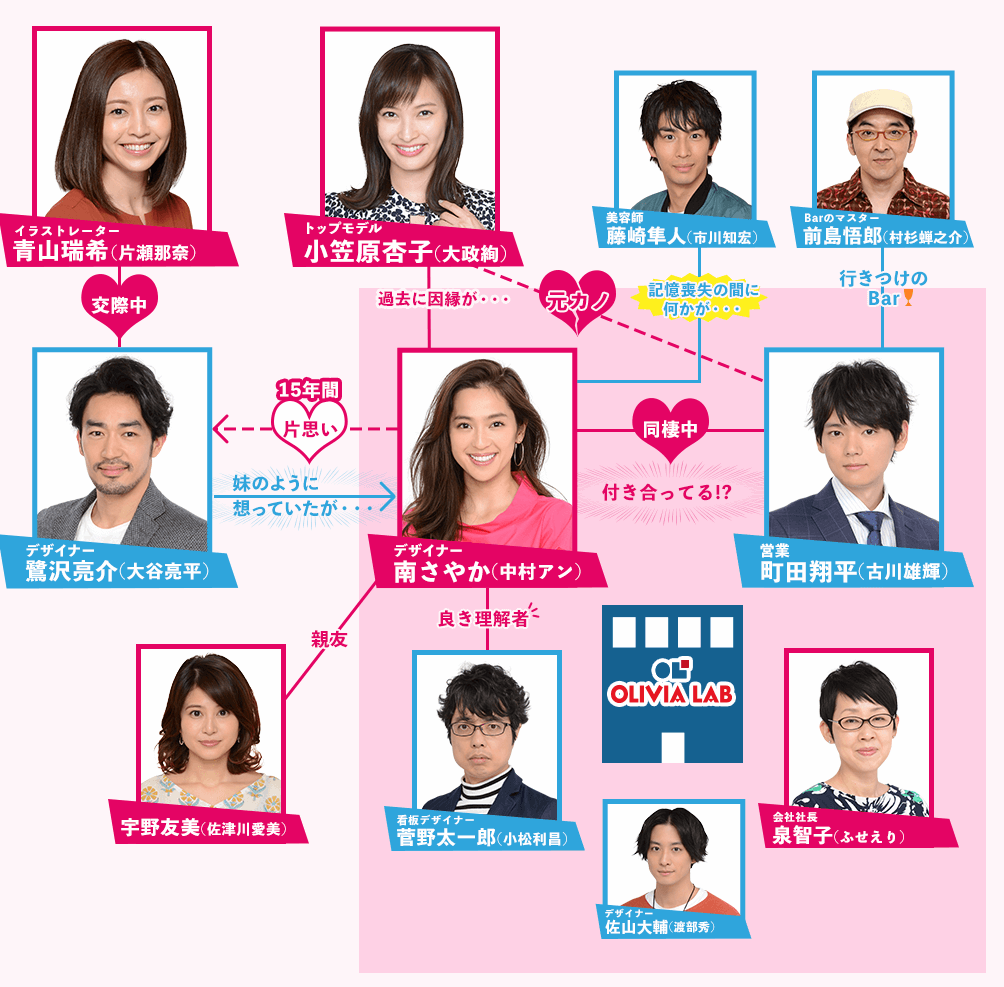
ラブリランのドラマ登場人物と相関図 原作との違いが出演者で一目瞭然 世界の名著をおすすめする高等遊民 Com

三角比の相互関係 証明 上の定義の図のように，三角比を とおきます。 (1) これらをもとの式の左辺へ代入しますと， となりますが，ここで，x2y2=r2 (三平方の定理を適用)なので，この式を上式へ代入すると， よって，sin2θcos2θ=1 が成り立つことが まずは王道の3つの三角関係について、どんな状況の関係のことを言うのか、それぞれ解説します。 現在、三角関係にある人は、自分がどの状況に当てはまるのか見てみてくださいね。 好きな人がかぶった 三角関係の中でも、一番多いのがこのパターンです。実験値（三角堰) 理論式（1），C=1340 三角堰公式 式（1） 0 50 100 150 0 250 300 350 400 0123 越流水深H(cm) 流量Q(cm 3 /s) 実験値（三角堰) 三角堰公式（1），C=1340 (a) tan()/ 2 2 5/ 2 15 8 θ gH と流量Q の関係 (b) 越流水深H と流量Q の関係 図16 堰で整理するグラフの例（三角堰の例

で表される3つの三角比の関数のことを、三角関数と言います。 「\(\sin{θ},\cos{θ},\tan{θ}\) の分母・分子をド忘れしそう」と感じる方も多いかもしれませんが、これらはその 頭文字 s,c,t の筆記体 のイメージと結びつけると覚えやすくなりますよ。三角比どうしの関係の例題でみたように、同じ角度に対する三角比の値は、互いにばらばらなものではなく、ある関係によって結ばれている。 以下では、この三角比の間に成り立つ関係を、一般的に導いてみよう。 （注） 図の直角三角形において \a=c\sin{A}~,~b=c\cos{A}\ であるから、$\tan{A}$ は 三角関数の公式その1 公式の1つ目は、 sin 2 θ cos 2 θ = 1 です。 つまり、下の図のような直角三角形を考えたとき、sinθの2乗とcosθの2乗を足すと1になるということです。

そこで、ここでは散布図のグラフウィザードを使って三角座標のグラフを作成してみます。 散布図は、縦軸（y軸）と横軸（x軸）からなるグラフなので、作成しようとする三角座標の構成点を全て x と y の座標で表示してそれらを散布図に描画すれば、三角座標グラフが作成できます。 三角比・三角関数の公式一覧。 正弦・余弦・加法定理など このページでは、 三角比・ 三角関数 の公式 をまとめています。 予習・復習に役立てていただければ嬉しいです。θ、y、rの関係図を示しました。 三角関数は三角比の考え方を発展させたものです。直角三角形の鋭角をαとするとき、各辺の比とαは下記の関係があります。これを「三角比（さんかくひ）」といいます。 三角比の詳細は下記をご覧ください。 三角比の定義は？1分でわかる定義、覚え方、表

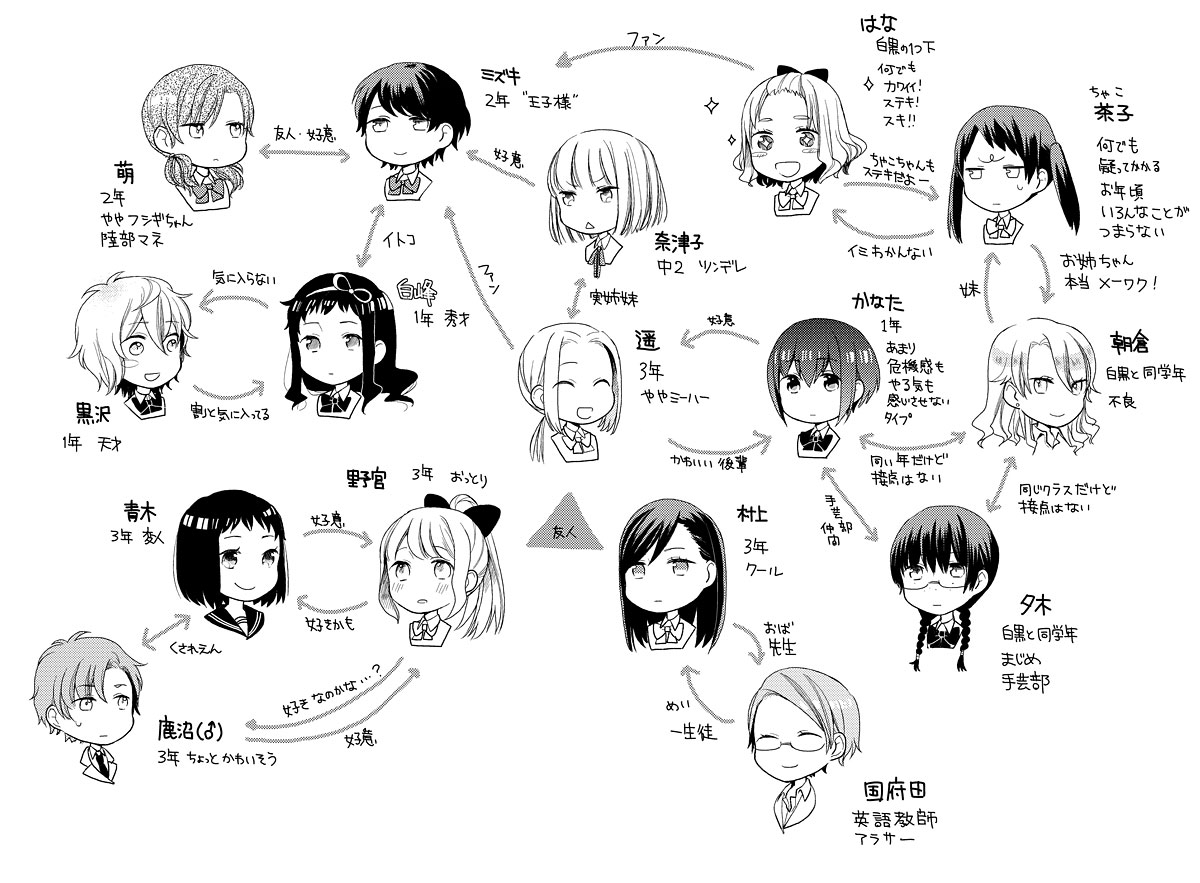
缶乃 三角関係入門 3 26 あのキス の超初期のキャラクター相関図です 知らないキャラがたくさんいる 白黒 瑞希萌はこの時点ですでに存在していて この頃は名前の関連付けにこだわってなかったので 瑞希と萌は名前につながりがないままになりました

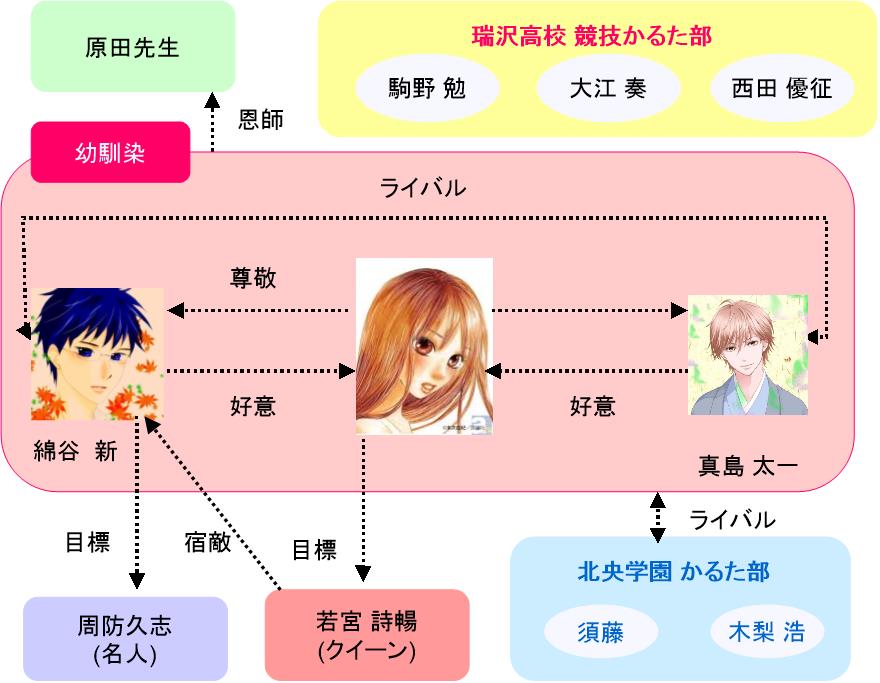
Honto ちはやふる 登場人物のキャラクターと人間関係の相関図

三角関数の公式一覧 このページでは、 高校学習レベルの三角関数の公式 を一覧にしています。 三角関数の定義をはじめ、三角関数の相互関係、周期性、加法定理、積和・和積、微分の公式を掲載しています。 また、三角形に応用したときの正弦定理や余弦定理も、図と共に掲載しています。 導出方法はみなさん自身でご確認の上、公式を確認してくださいねここでR は三角形ABC の外接円の半径である。 証明 外接円の中心をO とする。円周角と中心角との関係から 図のように∠BOC の大きさの半分がA になる。 A が鋭角,90 , 鈍角のどの場合についても BC の長さ = a =2RsinA が成り立つ。従って a sinA =2R である。同様にして b sinB三角関係図のPPTテンプレートの結晶組織 File Size KB ダウンロード回数 732 三角関係図のPPTテンプレートの結晶テクスチャ、図のダウンロード このPowerPointをダウンロードする 結晶 リング 三角

韓国ドラマナビ Jp

月刊少女 野崎くん が面白かった やっぱり漫画家さんは凄い 一般人の隠れ部屋

 三角関係に巻き込んでくる女子の特徴10パターン 三角女子その1 二番目でいいと思っている 言うまでもなく"二番目でいい"と考えている女子は不倫や浮気の対象になりやすく、泥沼の三角関係を起こしやすいです。 恐らく徒競走とかも"二位でいいや"という感じで適当に走ってきたの12 波としての三角関数 7 12 波としての三角関数 最初にも述べたように、このテキストでは時間t 秒 における信号値x(t) の関数を扱います。 したがって、周期関数の中で最も基本的な三角関数を、時間t 秒における信号値x(t)の関数に 書き換えましょう。⑴ 次の図で，sinθ，cosθ，tanθの値を求めよ。 ① ② ③ ④ ⑤ ⑥ ⑵ 右の図の直角三角形を用いて，次の値を求めよ。 ① sin30° ② cos30° ③ tan30° ④ sin45° ⑤ cos45° ⑥ tan45° ⑦ sin60° ⑧ cos60° ⑨ tan60° 2 三角比の相互関係① 次の問いに答えよ。ただし，θは鋭角

かわいい 無限に見ていられる ペンギンたちの 複雑な相関図 に注目集まる Grape グレイプ

虹オオカミ 今からでも間に合う 前半まとめ シリーズ史上最も熱い恋模様にハマる 涙の新章スタート 相関図 独占写真 モデルプレス

組織図やベン図など、プレゼンで概念や仕組みをわかりやすく伝えるには図表が欠かせません。パワポのSmart Artを使えば、驚くほど簡単にデザイン性の高い図表が作成できます。 執筆者：井上 香緒里 パワーポイントの使い方ガイド Smart Artで図表を手早く作る プレゼンのスライド作りに・直線や平面の平行や垂直の関係 ・見取図，展開図 ・ものの位置の表し方 ・面積の単位と測定 ・正方形，長方形の面積 ・角の大きさ 4年 ・図形の合同，多角形，正多角形， 円周率 ・角柱や円柱 ・三角形，平行四辺形，ひし形， 台形の面積 ・立体図形の体積 5年 ・縮図や拡大図 ・対称な三角形の合同条件・決定条件との関係（中学校の数学との関係） 図3、図4のような三角形において、二辺（ b , c ）とその間の角（ A ）が与えられると三角形は決まります。（三角形の合同条件・決定

1

三角関係

この図もドラッグで直角三角形を移動・変形できるが、 斜辺 の長さは一定になっている。 角度と cosθ と sinθ の変化の様子を観察しよう。 この図から容易に、cos 2 θsin 2 θ=1となることがわかる（斜辺がつねに長さ1であることに注意せよ）。 sin,cosが正になったり負になったりするが、 から に三面図の作図は，今後の機械製図のための練習である。 中心線やかくれ線などもしっかりと作図するように心がけたい。 44 三面図の必要性 以下，第三角法による三面図は実際の機械図面でどのように使われるのか，また，なぜ重要なのか，いくつかの（鋭角 に対する）三角比の基本関係式 上の直角三角形において， （a とc の関係） a = csin ， c = acsc (= a sin ) （b とc の関係） b = ccos ， c = bsec (= b cos ) （a とb の関係） a = btan ， b = acot (= c tan ) (1)ただし， ，， などの角の大きさには制限がつく。 (2)一般的に，三角関数の相互関係sin2 cos2 = 1 は「三平方の定理」から導出する。また，その他の諸公

ラブセラピーのキャスト相関図一覧 出演者を画像付きで関係図もご紹介 韓国ドラマ動画配信ギャラリー

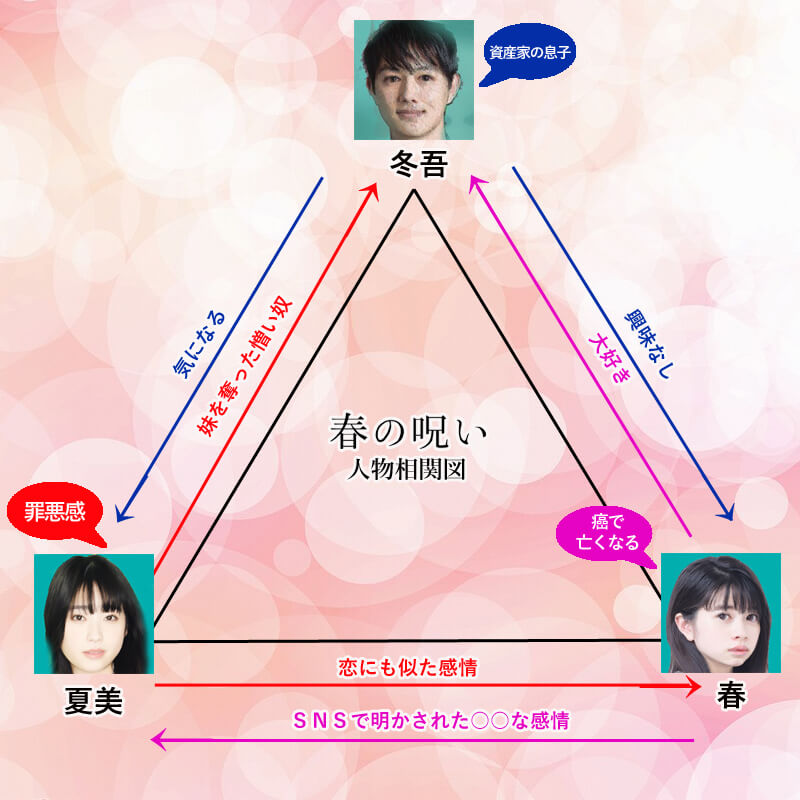
ドラマ 春の呪い 相関図 キャスト春 冬吾 夏美は 原作の結末

座標と三角比の関係 単位円 単位円 座標平面上の原点 $\text{O}$ を中心とする半径 $1$ の円を単位円 (unit circle) という。 三角比は、この単位円を用いて（$90^\circ$ 以上に）拡張される。 三角比の拡張について （注） 三角比の定義を、斜辺が $1$ である直角三角形 $\text{OPQ}$ において考えて 相互作用図はシーケンス図とコラボレーション図からなります。 参考文献 『まるごと図解 最新 オブジェクト指向がわかる』、河合昭男ボロノイ図，デローネイ三角形分割 ボロノイ図とは ・平面上に多数の点が与えられたとき，平面をどの点に最も近いかという 関係で分割したものをボロノイ図(Voronoi diagram)という． ・2点だけの場合 2点の垂直2等分線による分割 ・3点の場合 3点で決まる三角形の外接円の中心から各辺に引いた

1

京都でペンギンの ややこしい 相関図が話題に 禁断愛や種を超えた三角関係も 烏丸経済新聞

日向坂で会いましょう 最新メンバー相関図を作ろう 乃木坂46 櫻坂46 日向坂46 眺めてるだけで十分 笑

33 韓国tvドラマガイド別冊 最新ドラマ相関図ガイド19 発売 Tabilista タビリスタ

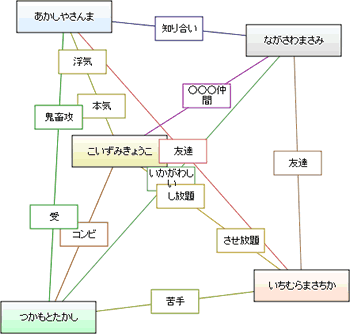
相関係図ジェネレータで分かる芸能人の人間関係

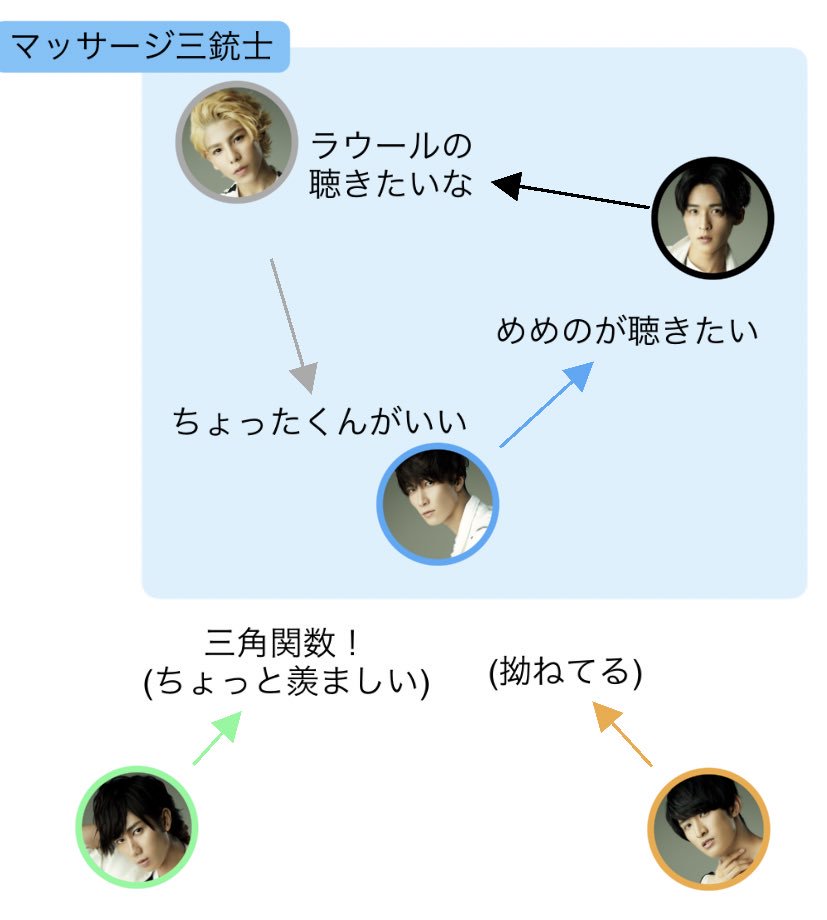
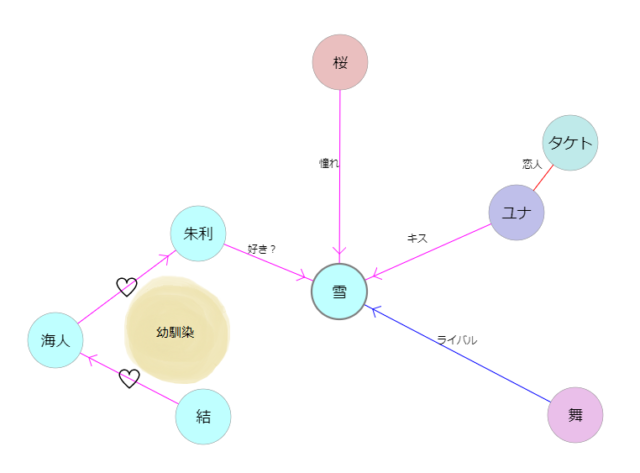
雪見りんご على تويتر 今夜の主観的相関図はこういうことでいいですか 素のwoman

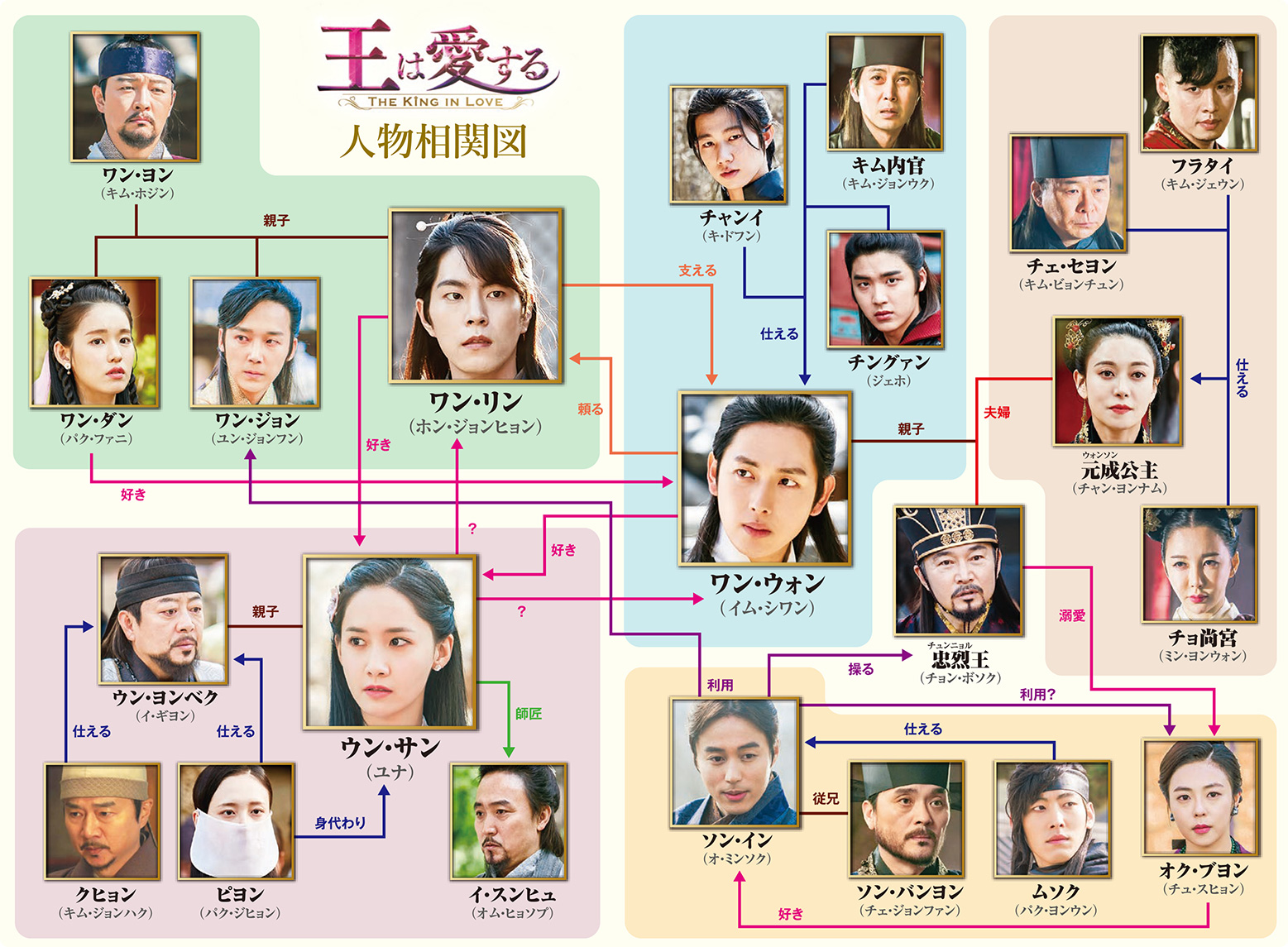
王は愛する 特設サイト

かぐや様は告らせたいは告らせたいの相関図 恋愛要素 関係や告白 キスシーン 誰と誰が付き合うかまとめ マンガアニメをオタクが語る

高校 数学 三角比８ 相互関係 図 12分 Youtube

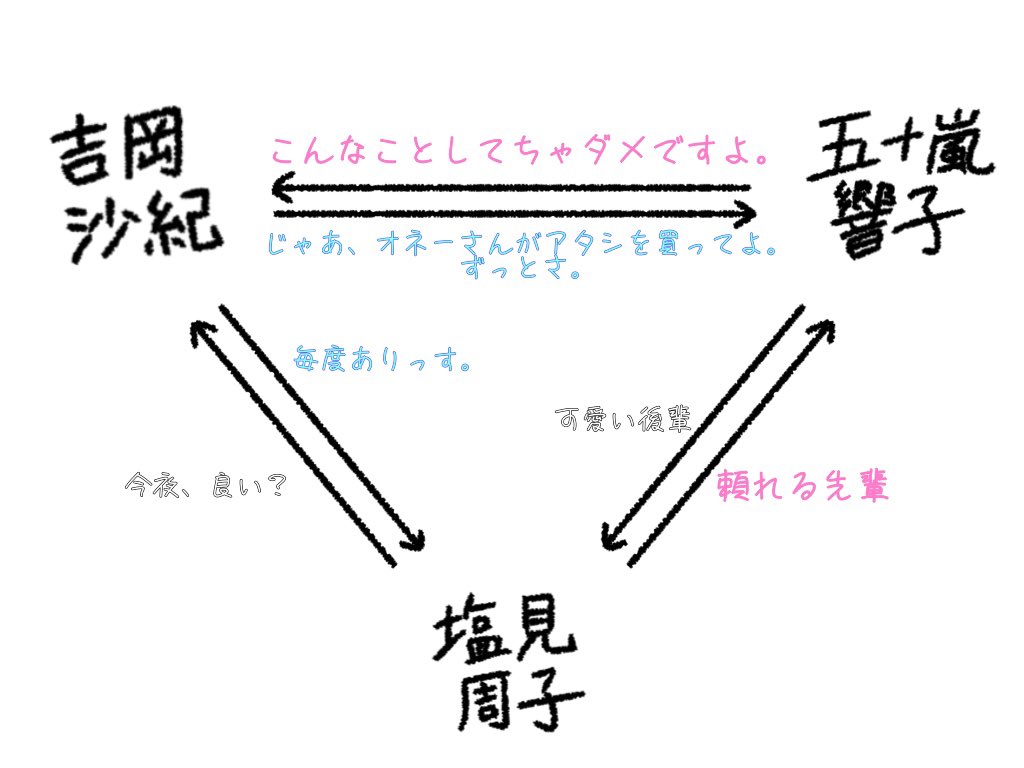
ট ইট র Morukyon しょうもないことばっかり考えて生きてる これは売春してる吉岡さんと会社勤め五十嵐響子さんと五十嵐さんの先輩で吉岡さんの常連客の塩見周子さんの三角関係 恋愛ドラマの撮影の相関図です T Co Ed73fzyl6w ট ইট র

京都水族館の複雑すぎる ペンギン関係 の図解が話題 浮気 禁断の恋 全59羽のドラマが見える 三角 関係 相関 図

Eclipseのemfモデルを使用したgefアプリケーションの作成 Codezine コードジン

三角関係図 サイエ Cayest

三角関係 アイコン素材ダウンロードサイト Icooon Mono 商用利用可能なアイコン素材が無料 フリー ダウンロードできるサイト

中国 華流 ドラマ 燕雲台 相関図とキャスト情報

高校数学 三角比の相互関係1 図の利用 映像授業のtry It トライイット

三角関係に巻き込まれました 下の図を見ていただけると分かる通り私は Yahoo 知恵袋

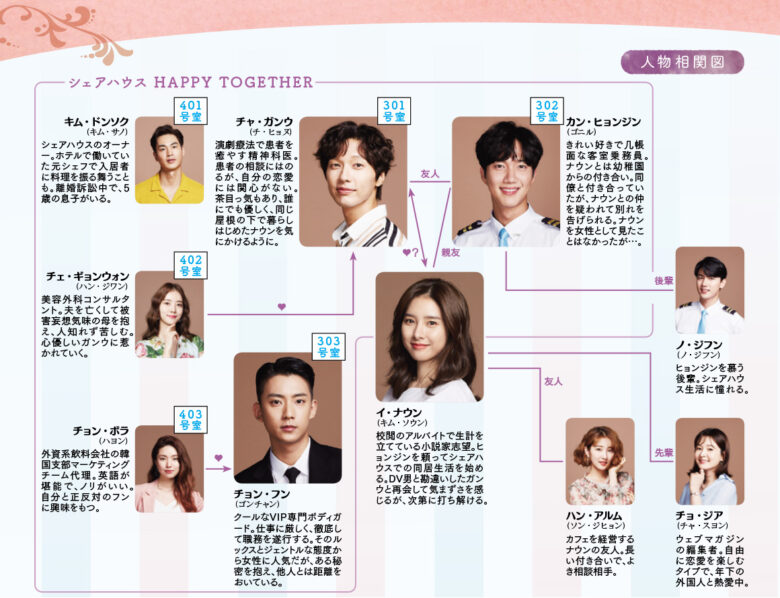
韓国ドラマ 恋愛は面倒くさいけど寂しいのはイヤ 相関図とキャスト情報

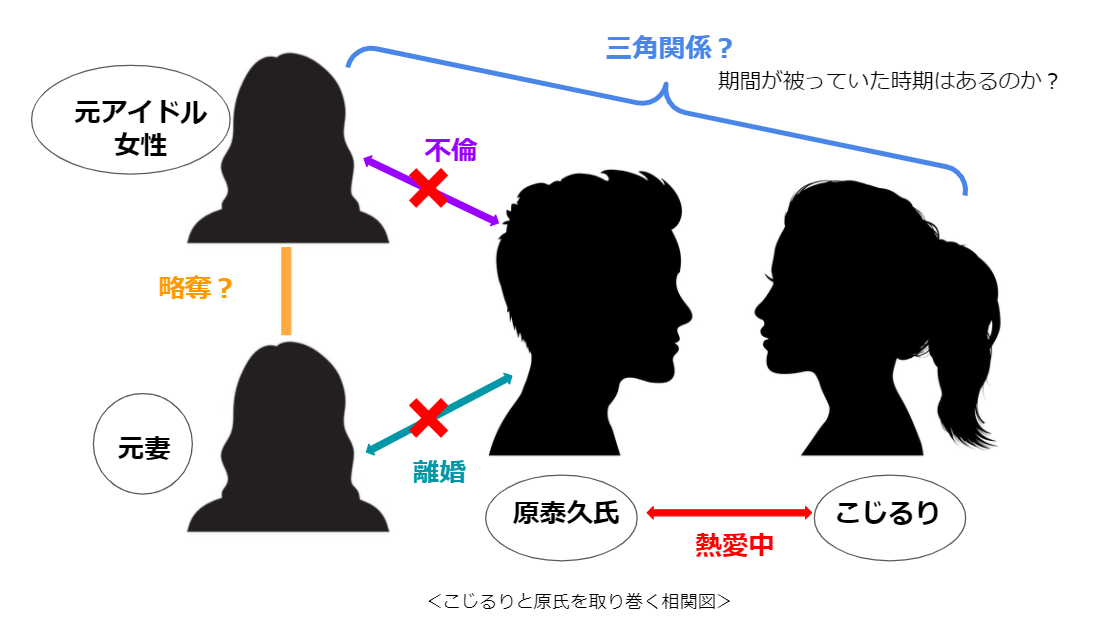
こじるりの泥沼恋愛と 女の戦い そのドロドロぶりが相関図と年表で明らかに まぐまぐニュース

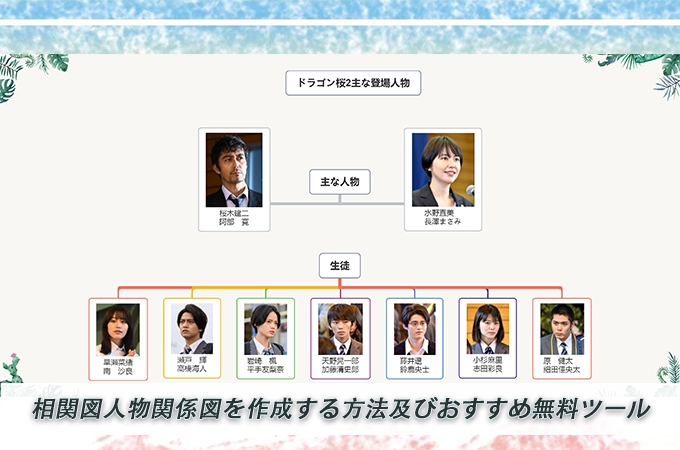
誰でも手軽に相関図を作成できる無料ツール及び相関図作り方の紹介

漢方医学の 二日酔い の理論とその対策内容が興味深いです Enjoy Herbal Life

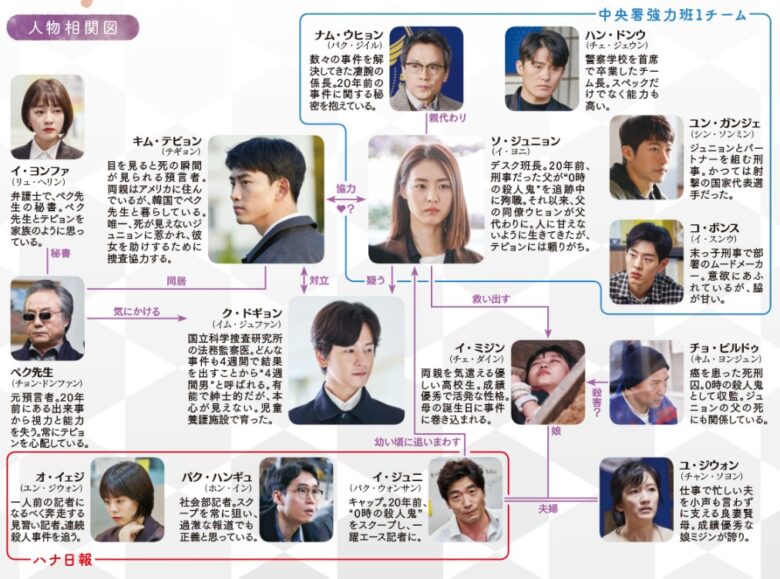
韓国ドラマ ザ ゲーム 0時に向かって 相関図とキャスト情報

7羽の手乗り文鳥 フジオとフジコ 相関図 を作りました 文鳥 相関図 イラストポスター

誰でも手軽に相関図を作成できる無料ツール及び相関図作り方の紹介

薬屋のひとりごと 小説7 8巻の感想と相関図 のんびり少女漫画語り

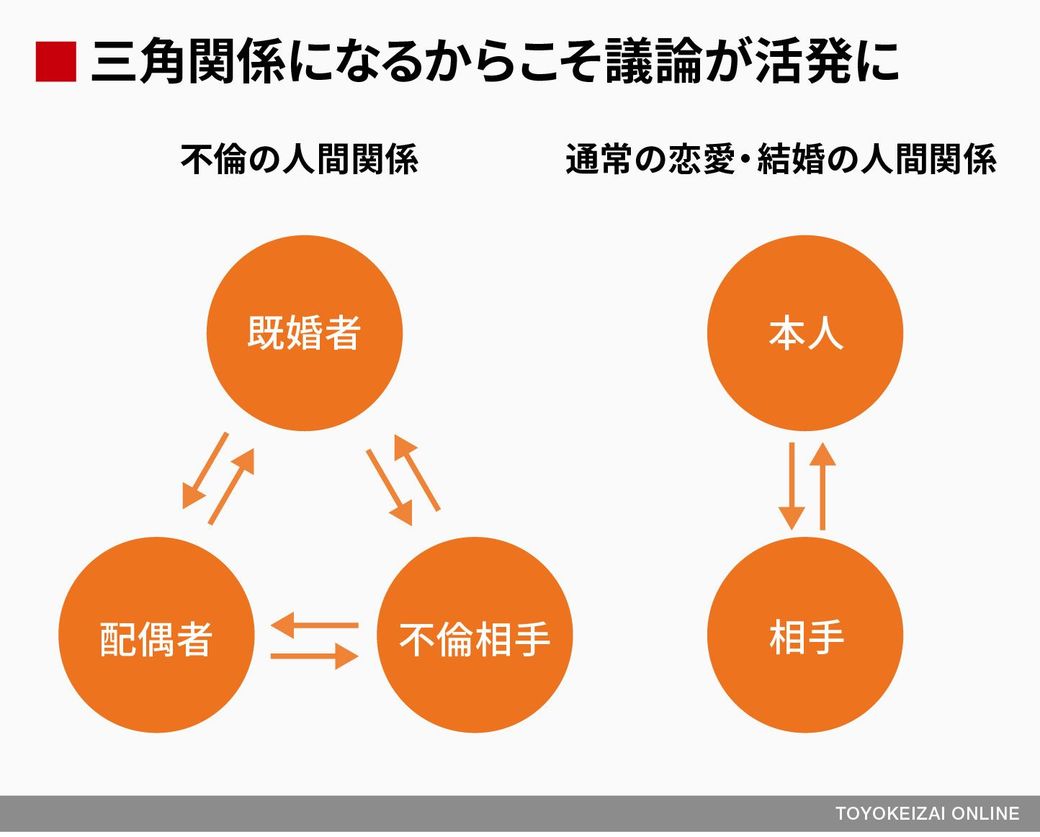
不倫がこんなにも世の中の関心事になる理由 メディア業界 東洋経済オンライン 社会をよくする経済ニュース

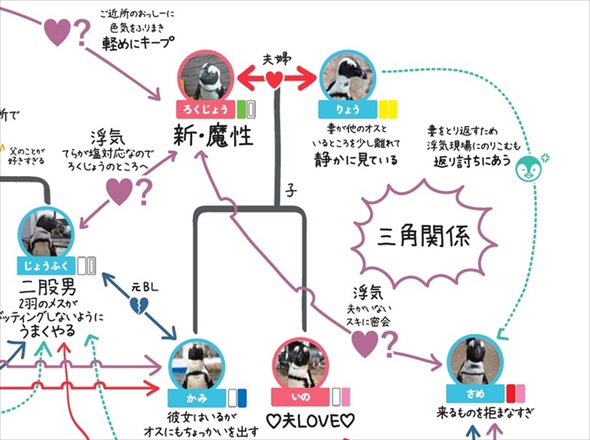
昼ドラ並みのドロドロ感 京都 すみだ水族館のペンギン相関図がますます複雑に 1 2 ページ ねとらぼ

私の試験研究 農業技術センター病害虫部 主席研究員 八瀬 順也

1

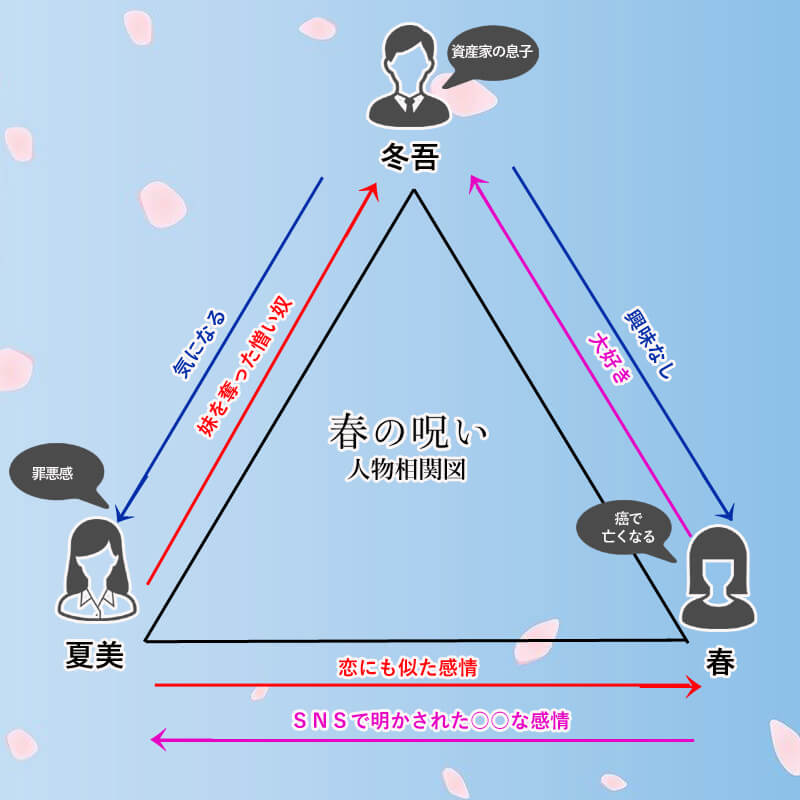
春の呪い 原作のネタバレ 夏美と冬吾が選んだ結末は

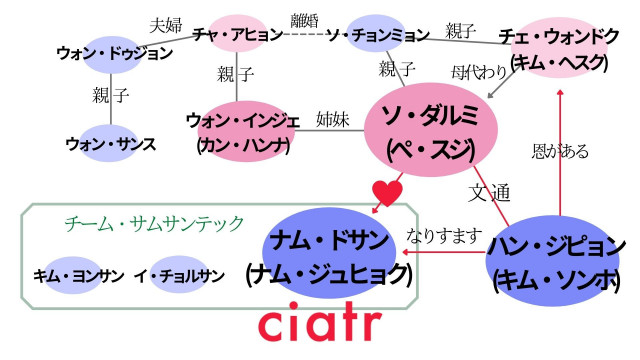
韓国ドラマ スタートアップ 夢の扉 キャスト 登場人物一覧 あらすじや視聴率も Ciatr シアター

三角関係の力学 龍の吐息

人間関係などの相関図が無料で作成できるお勧め6個のツール イズクル

京都水族館の複雑すぎる ペンギン関係 の図解が話題 浮気 禁断の恋 全59羽のドラマが見える ライブドアニュース

人材派遣ってなぁに 上手な退職 下手な退職

ラブリランのドラマ登場人物と相関図 原作との違いが出演者で一目瞭然 世界の名著をおすすめする高等遊民 Com

韓国ドラマあらすじおすすめ Jp

三角関係の写真素材

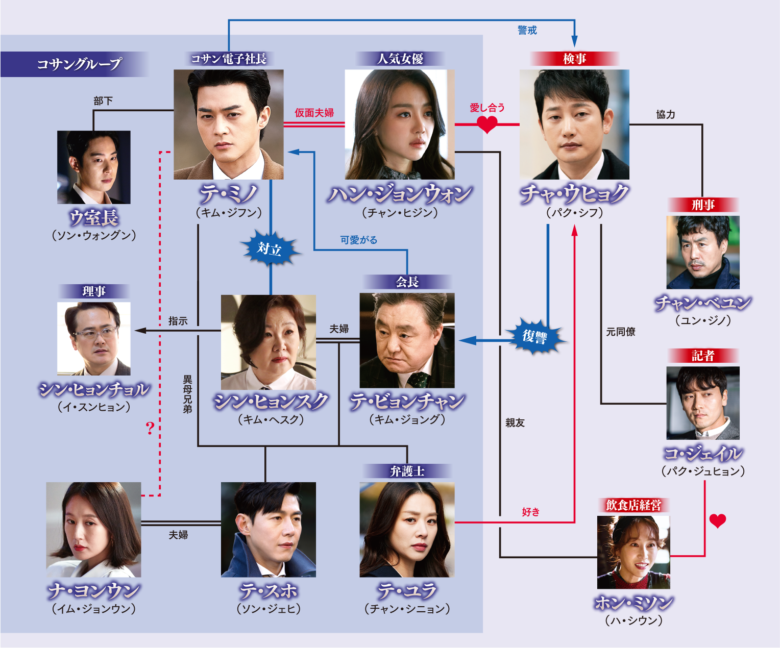
韓国ドラマ バベル の相関図とキャスト情報

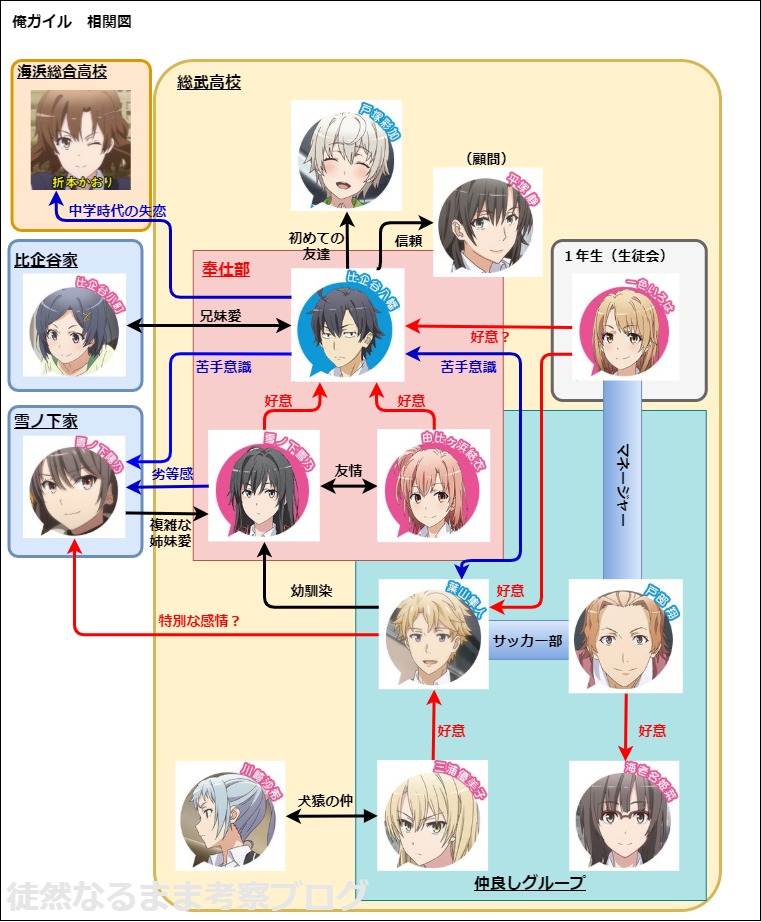
俺ガイルの人物相関図 登場人物 キャラクターの一覧を解説

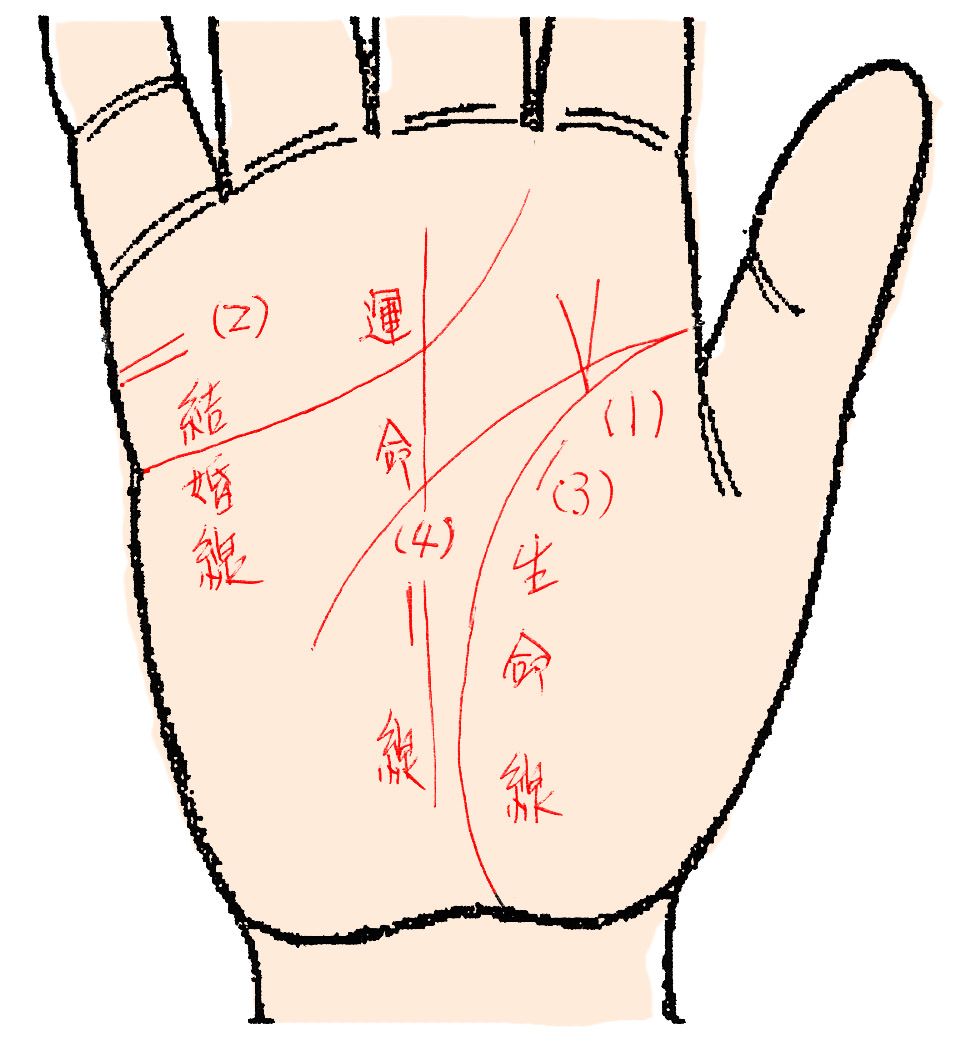
手相の話題59 三角関係を招きやすい 三角関係の相 達人に訊け 中日新聞web

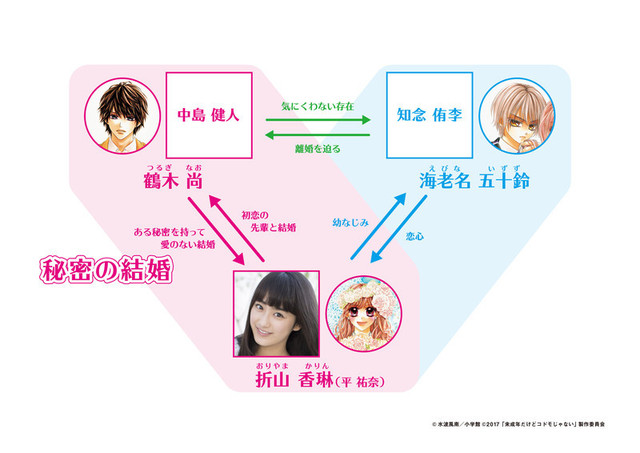
中島健人 平祐奈 知念侑李 未成年だけどコドモじゃない 映画化で究極の三角関係 映画ニュース 映画 Com

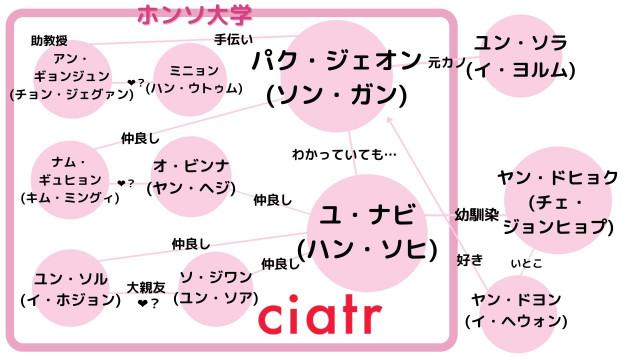
わかっていても キャスト 相関図とostを紹介 あなたの推しカップルは Ciatr シアター

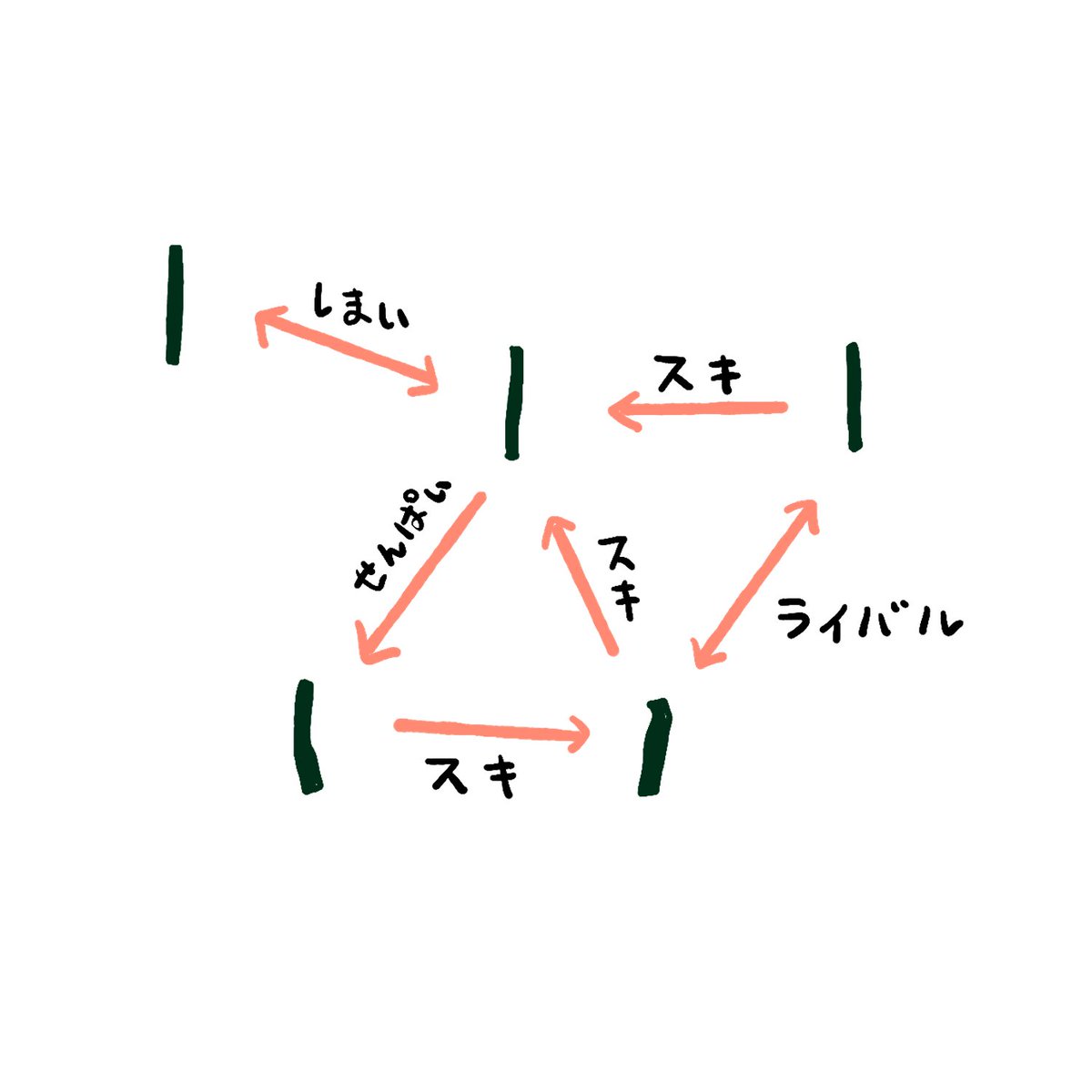
Study 反省 きざみのり の 相関図

誰でも手軽に相関図を作成できる無料ツール及び相関図作り方の紹介

広告コミュニケーション 三つのメディアと三角関係 概念図 デジタルマーケティング マーケティングのアイデア

星新一 三角関係 泉獺のどうでも映画批評

漫画無料ziprar Site

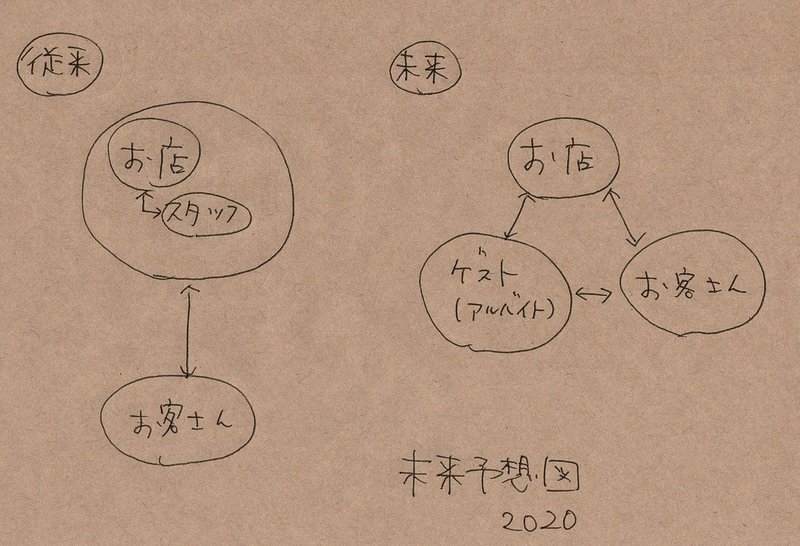
未来予想図 幸せな三角関係 Upskch Note

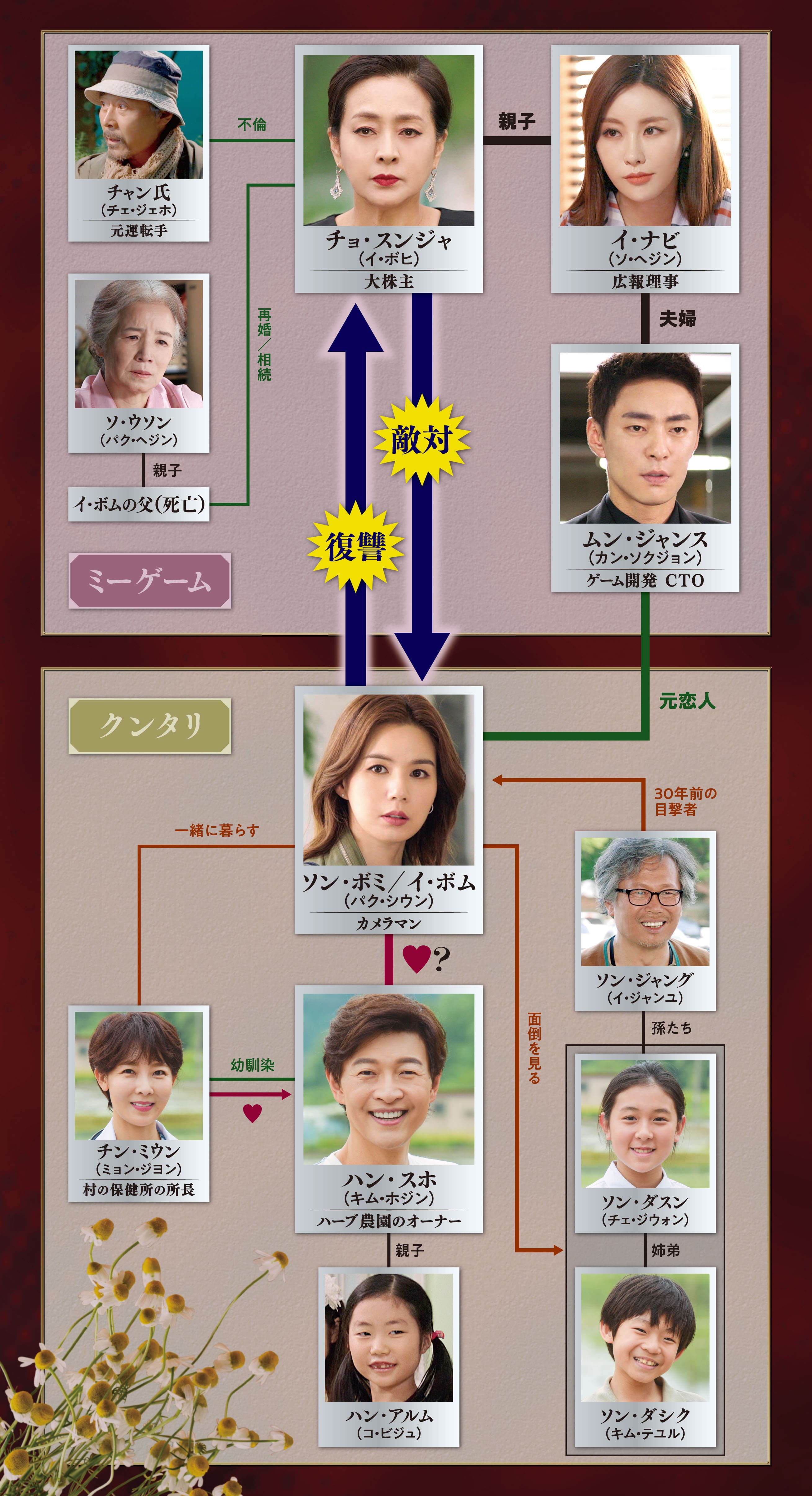
逆境の魔女 シークレット タウン 公式サイト

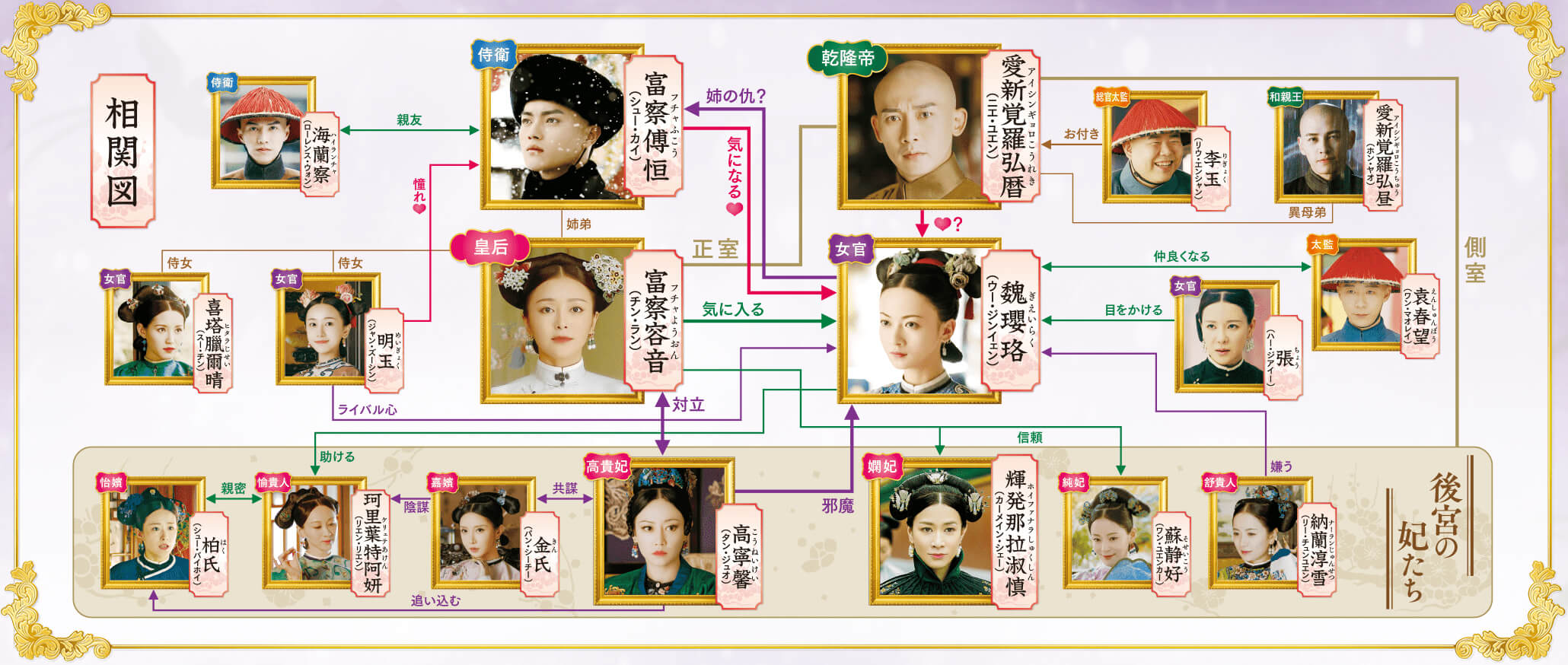
瓔珞 エイラク 紫禁城に燃ゆる逆襲の王妃 無料動画 相関図 キャスト 中国ドラマ 楽天tv

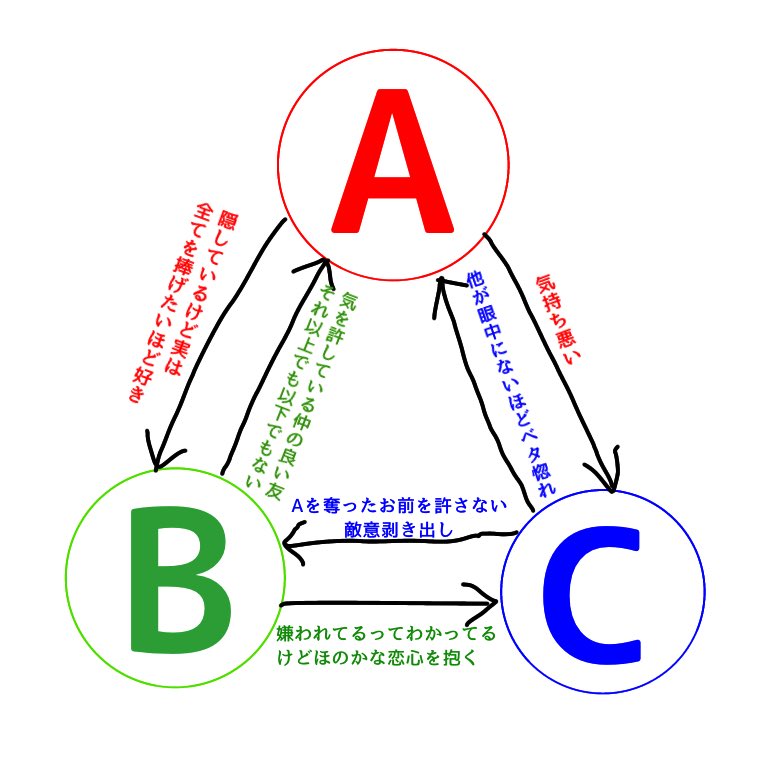
話は大体わかったカサ子 على تويتر こういう三角関係があったとして じゃあこのa Cの中で誰か一人死ぬってなったら 誰をころすかでその人の性癖がわかってしまうと思うんだなあ みつを

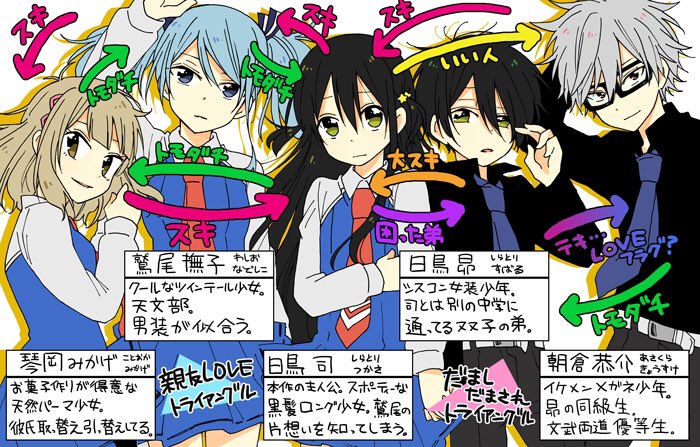
小林 キナ Ar Twitter とてもわかりやすい人物相関図です ダブル三角関係からなる五角関係物語

ジェノグラム エコマップの簡単書き方ガイド Lucidchart

相関図作成ツールに機能を追加した 相関図作成ツールをつくってみた 人物相関図とか

大阪 京都 兵庫は複雑な三角関係 元住民が作った相関図が 大体あってる と話題に

どんな 三角関係 タイプ診断 Mirrorz ミラーズ 無料の心理テスト 診断 占い

コンペ 小豆島 のアイデア 11 件 小豆島 デザイン 波 絵

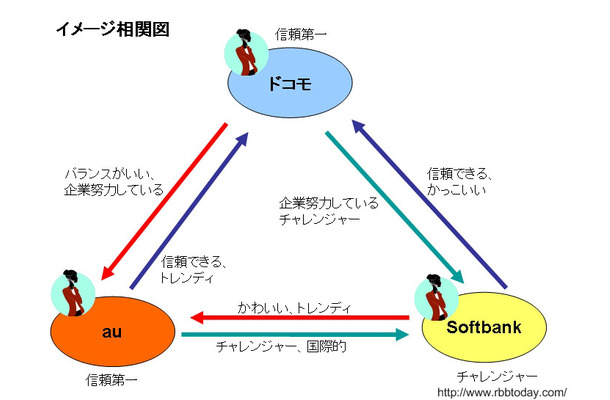
ユーザが抱く携帯キャリアのイメージ その 三角関係 とは ネットエイジア調べ Rbb Today

四角関係 の読み方に関する一考察 あとーすログ

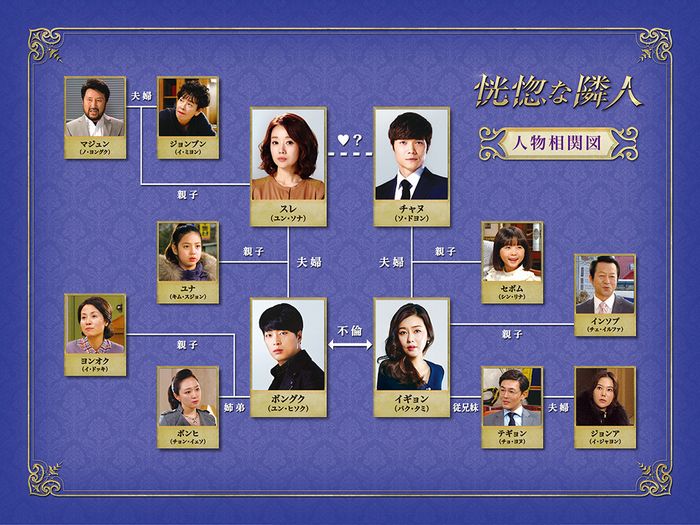
恍惚な隣人のキャスト 出演者 人物相関図 登場人物まとめ ユン ソナが不倫 三角関係どころじゃないドロドロの愛憎劇ドラマ ベラスパ Belluspa

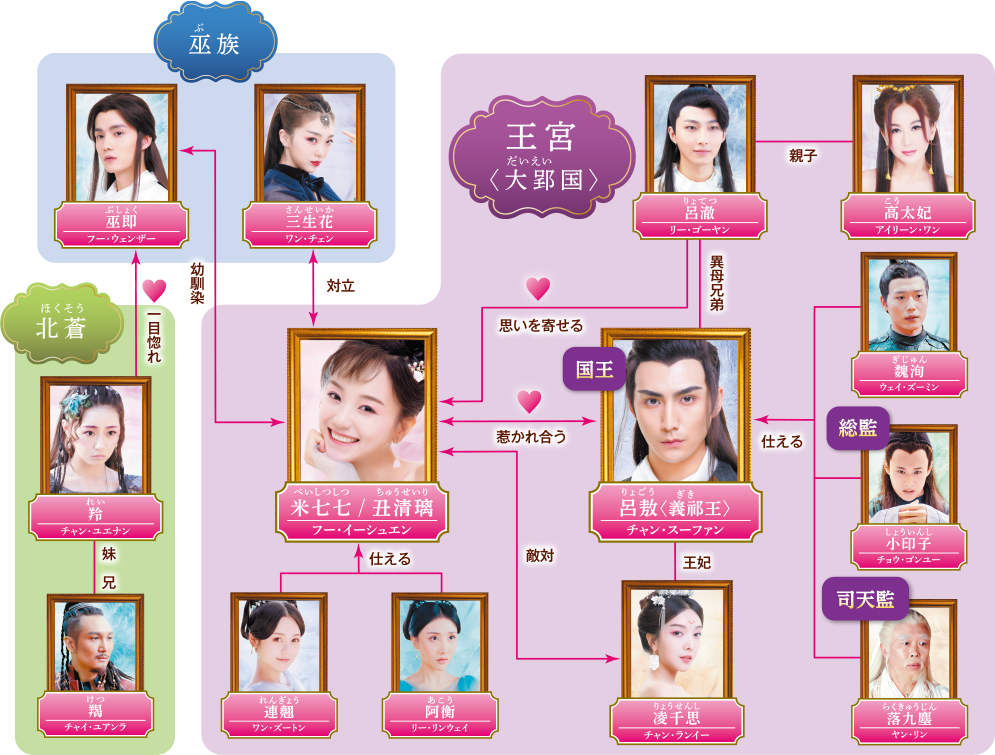
親愛なる君主様

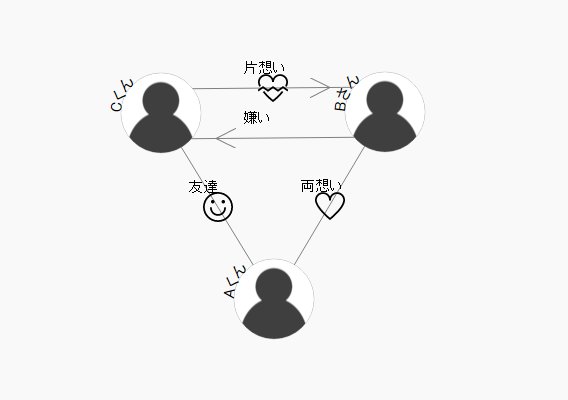
相関図作成ツールのご利用ありがとうございます

画像 写真 非婚主義のヒロインにモテ期到来 三角関係ラブコメ あいつがそいつだ アマプラで配信 7枚目 Oricon News

三角関係図のpptテンプレートの結晶組織 Powerpointテンプレート無料ダウンロード

大阪 京都 兵庫の3地域は複雑な関係 相関図がtwitterで話題 ライブドアニュース

韓国ドラマ ただひとつの愛 相関図とキャスト情報

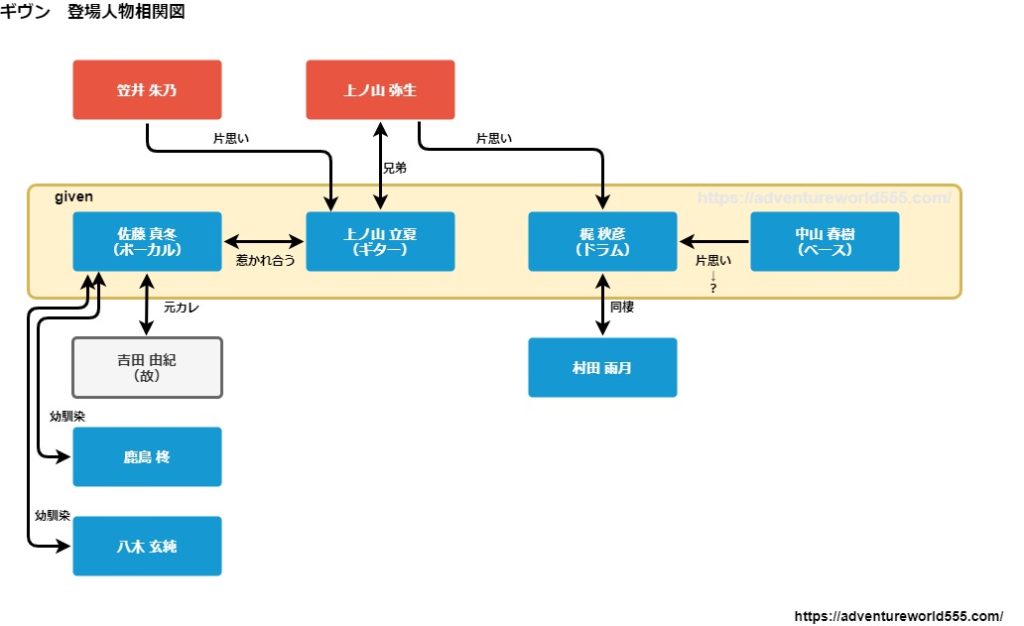
ギヴンの人物相関 登場人物 カップリングの組み合わせと受けはどっちかも考察

Blに関する質問 A B や A B C などの関係性を表す表記は Wikipediaより 人力検索はてな

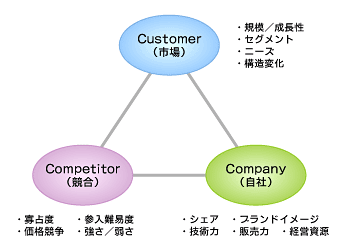
人物相関図 を描いてみよう 3c分析 経営戦略に学ぶ自分戦略 1 It

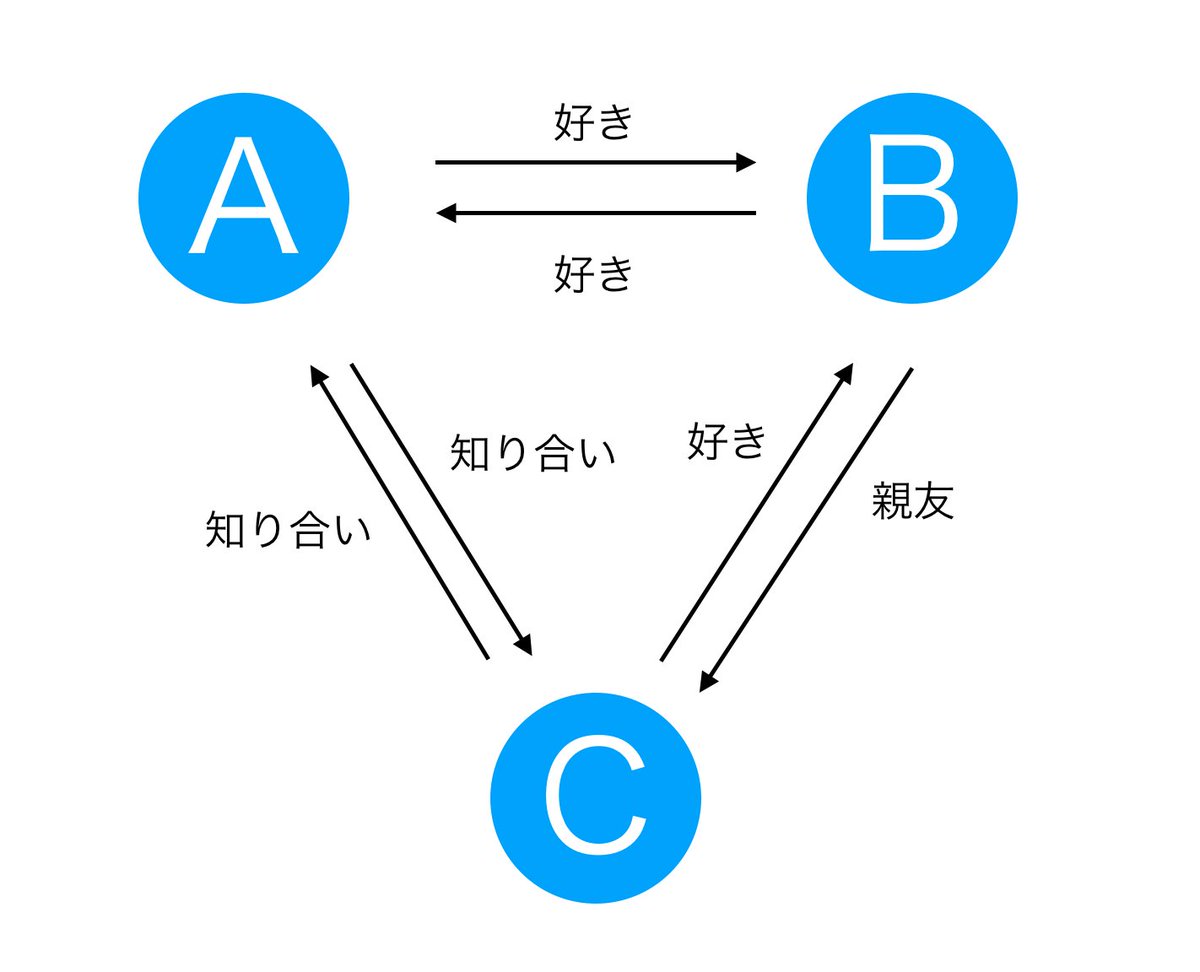
みつえもん No Twitter スタァライトのひかり 華恋 まひるはそれぞれこの図のa B Cに値するとは常々思っていますが この性癖がバレる 三角関係図のbc関係に値するものは他作品でいうと やが君の燈子と沙弥香なので それらと比較すると関係的にはまだ弱いと思うん

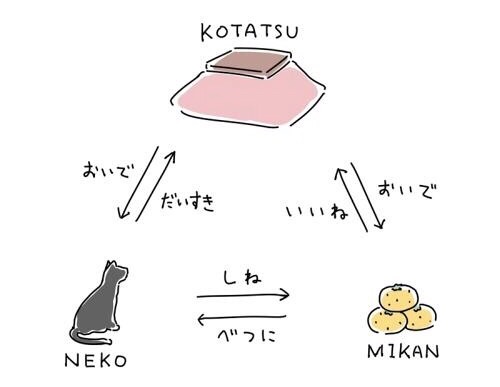
冬の大三角 猫とこたつとみかんの相関図 ねこナビ

ルームメイト 人物相関図 Shampooになりたい Afterschoolに夢中

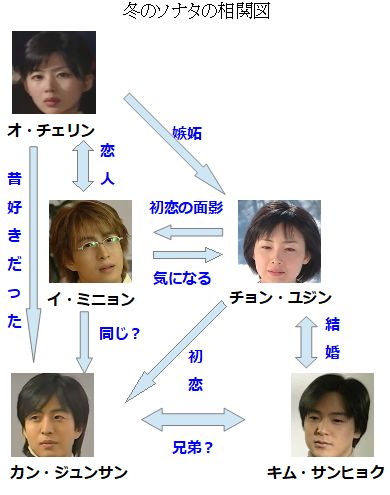
冬のソナタと死の真相 口コミやあらすじネタバレ相関図

Gandam5document

魔性の女 浮気の返り討ちにあった男 今年もペンギン関係は 愛憎ドロドロ 京都水族館が相関図を更新 まいどなニュース

モンスト攻略 11月3日より新イベ 防衛軍vs昆虫型戦闘兵機 初の相関図公開で三角関係の恋愛あり 本編でもストーリーは楽しめるのか アプリ学園

三角関係の構造 笑 Georgie717のブログ

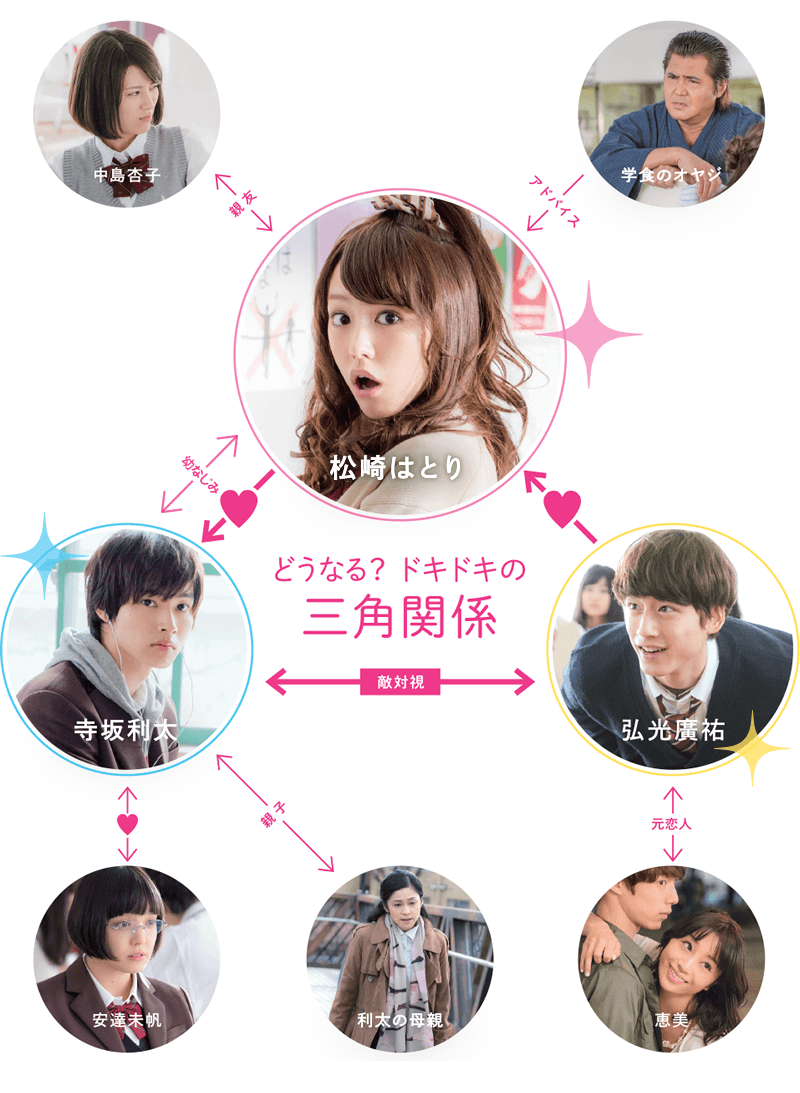
映画 ヒロイン失格 人物相関図

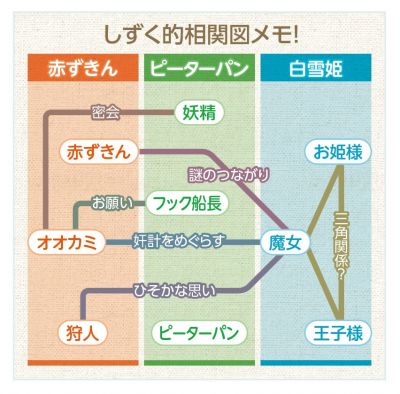
ニュース ラブライブ 虹ヶ咲学園スクールアイドル同好会

韓国ドラマ マイシークレットホテル あらすじ 全話一覧 相関図 キャスト Dvd 韓国ドラマのあらすじ 韓国ドラマのネタバレ 放送予定

私の周りの三角関係図 Twitter Search

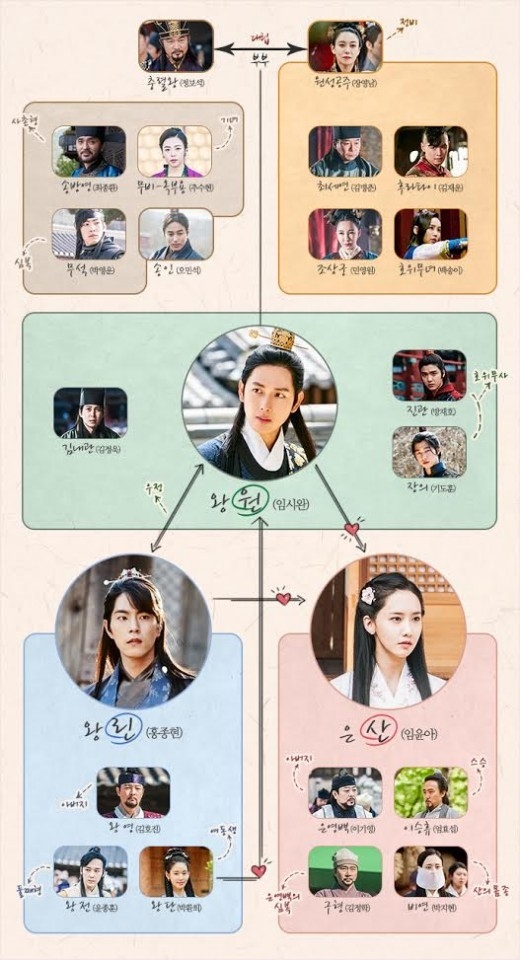
Ze A シワン 少女時代 ユナ ホン ジョンヒョン出演ドラマ 王は愛する 人物相関図を公開 愛と欲望の三角関係を予告 Kstyle

相関図あり 最高の結末 ひるなかの流星 のあらすじ 見どころ 微ネタバレ 少女漫画博士うららか

３６０ 都構想 首相発言のなぜ 迫る総裁選 大阪自民 維新と 三角関係 朝日新聞デジタル

Uzivatel めじろ Na Twitteru 東リベのクソめんどくさい三角関係 場地 千冬 一虎 相関図です 自己解釈あり 少しネタバレ 見てくれ 文字数が多くてキモい

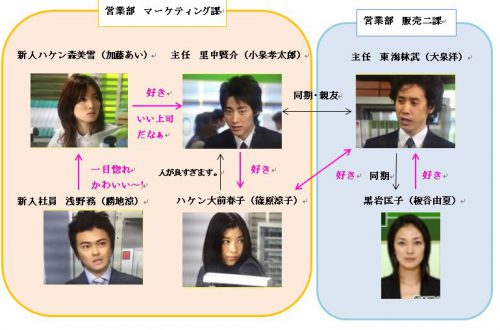
恋愛相関図あり 恋愛部分のみパパっとネタバレ ハケンの品格1 大前春子 東海林 里中の三角関係結末は 最終回でどっちとくっついた

ましろのおとに恋愛要素はある 相関図も解説 放映中のアニメ制作会社と海外の反応もご紹介 民謡応援ファンサイト つなぐ

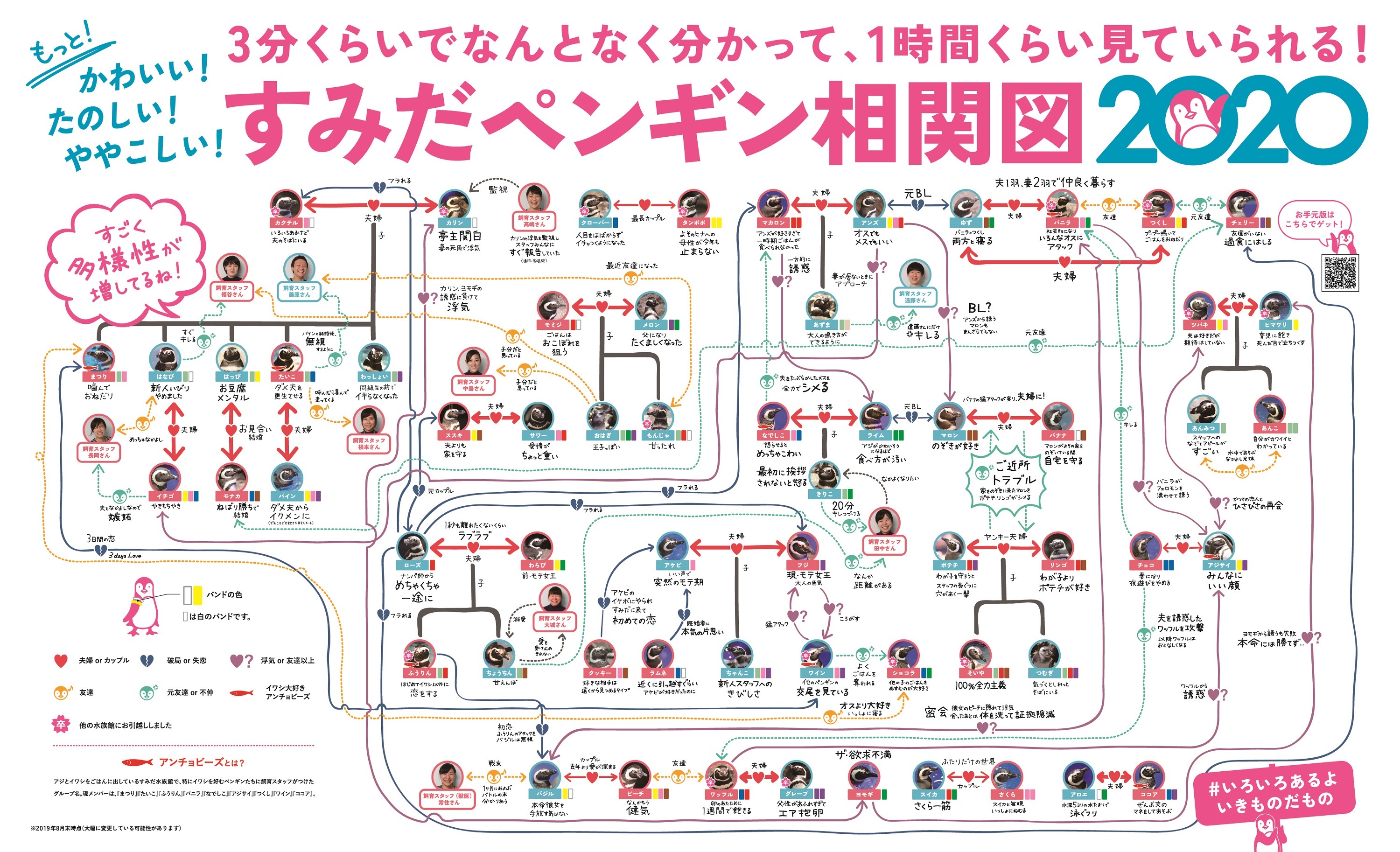
すみだ 京都水族館 ペンギン相関図 展示開始 ペンギンたちの多様な関係性が話題に Advanced By Massmedian アドバンスト ちょっと先の価値観を見つけるメディア

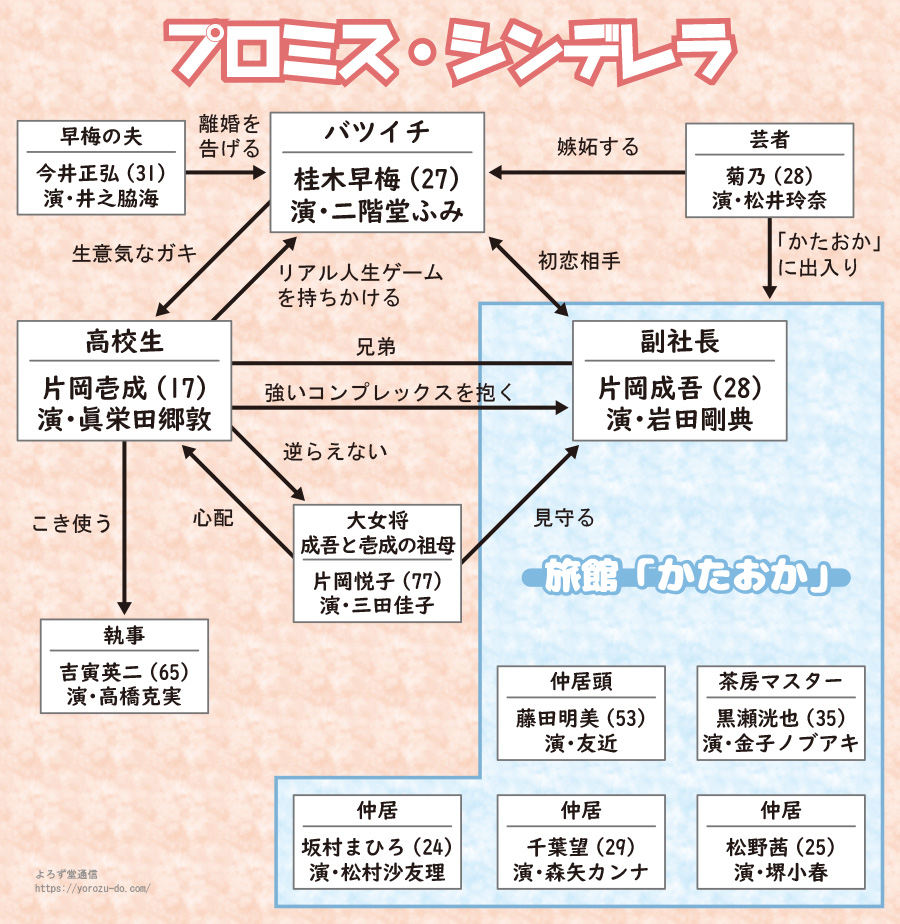
プロミス シンデレラ ドラマ相関図とキャストは 二階堂ふみが三角関係に よろず堂通信

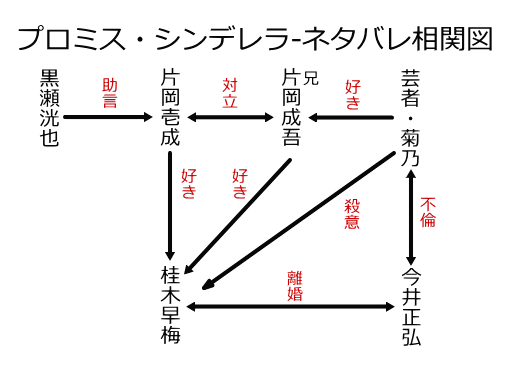
プロミス シンデレラ 原作と最終回のネタバレと相関図

韓国ウェブドラマ トップマネジメント の相関図とキャスト情報

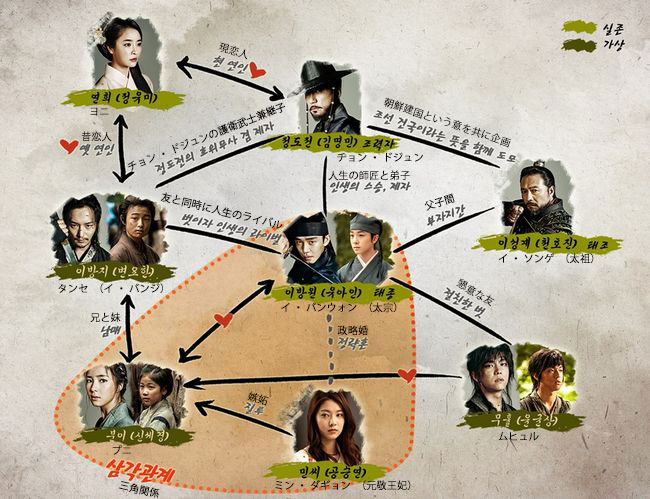
六龍が飛ぶ 人物相関図 続 同好大長今的 六龍が飛ぶ ドラマガイド

韓国ドラマあらすじおすすめ Jp